NeetCode 150: Search in Rotated Sorted Array

Table of contents

The Problem

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

The Approach

The goal is to locate the pivot, & then determine which half of the array to search. We have to run 2 sets of Binary Search to achieve this.

The first set searches for the pivot value.

By comparing target to this pivot value, we then determine which half to search.

The second Binary Search searches for target & returns -1 if it does not exist.

My Solution

class Solution {
    public int search(int[] nums, int target) {
        int maxBound = nums.length - 1;
        int minBound = 1;
        
        // 1st BS to locate the pivot.
        if (nums[0] == target) {
            return 0;
        }

        while (maxBound >= minBound) {
            int midIndex = (maxBound + minBound) / 2;

            if (nums[midIndex] == target) {
                return midIndex;

            } else if (nums[midIndex] >= nums[0]) {
                minBound = midIndex + 1;

            } else {
                maxBound = midIndex - 1;
            }
        }
        int pivot = Math.min(maxBound, minBound);

        // Determines which half (before or after pivot) to search. If 
        // target is both smaller than the pivot value & nums[0], it
        // only can exist in the left half (i.e after the pivot).
        if ((target < nums[pivot]) && (target < nums[0])) {
            maxBound = nums.length - 1;
            minBound = pivot + 1;
        } else {
            maxBound = pivot - 1;
            minBound = 0;
        }

        // 2nd BS to search for target in the chosen half.
        while (maxBound >= minBound) {
            int midIndex = (maxBound + minBound) / 2;

            if (nums[midIndex] == target) {
                return midIndex;

            } else if (nums[midIndex] > target) {
                maxBound = midIndex - 1;
                
            } else {
                minBound = midIndex + 1;
            }
        }
        return -1;
    }
}

We then initialize maxBound & minBound, at the opposite ends of the array. Note that minBound = 1 as nums[0] is the value that nums[midIndex] is being compared to.

For each iteration of the loop, we determine the midIndex. This value is then compared to nums[0] & there are two outcomes:

• If nums[midIndex] >= nums[0]: The pivot lies in the forward direction, set minBound = midIndex + 1.
• If nums[midIndex] < nums[0]: The pivot lies in the backward direction, set maxBound = midIndex - 1.

At the end of the Binary Search, we locate the pivot’s index using Math.min(maxBound, minBound).

We then compare target to the pivot value. To illustrate this comparison, let us look at an example;

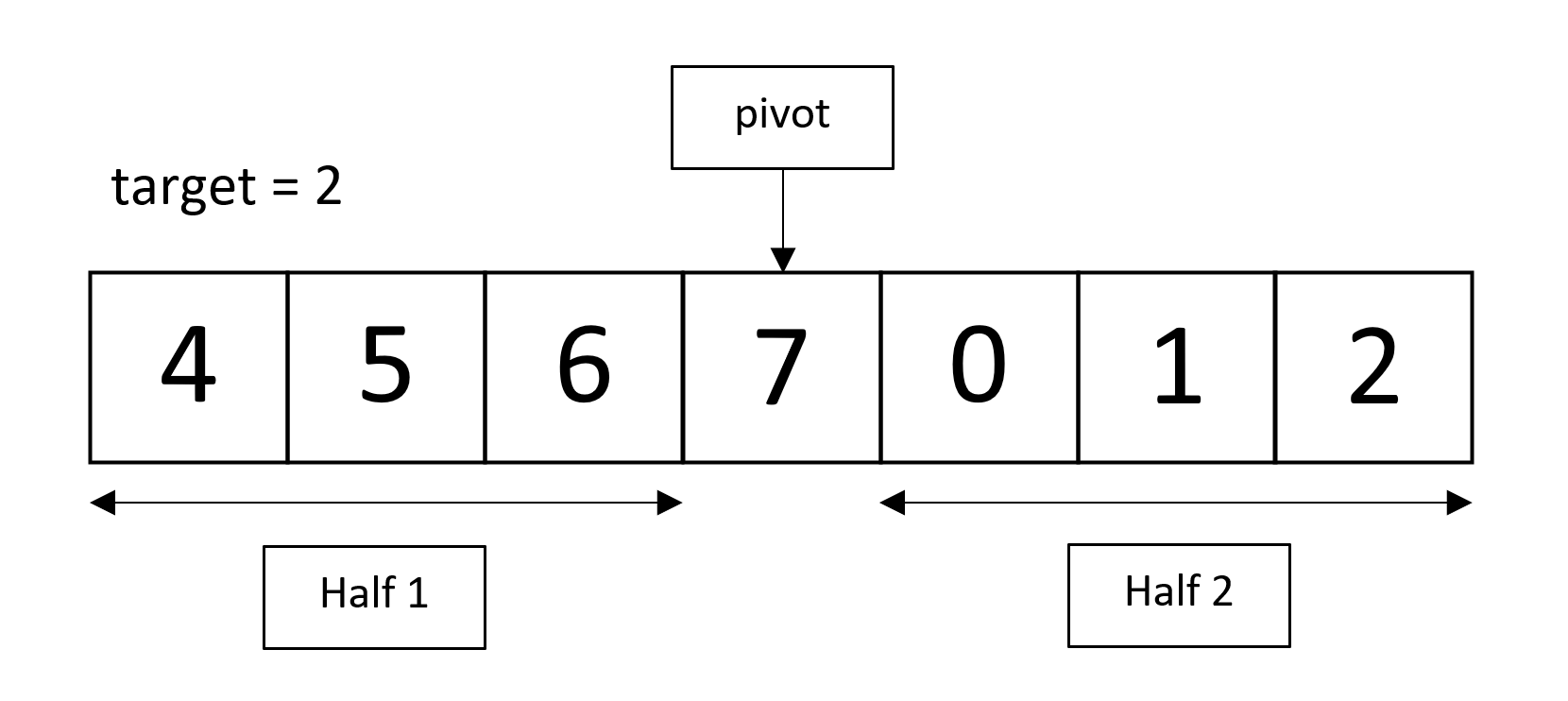
Illustration created by me.

Through this comparison, (i.e. 7 > 2), target could possibly be in both halves. With the additional comparison with nums[0] (i.e. 4), we narrow down the search space to ‘Half 2’, & then apply Binary Search to locate this value, returning -1 if it is not found.