Table of contents
Open Table of contents
The Problem
Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.
The overall run time complexity should be O(log (m+n)).
| Example 1 | Example 2 |
|---|---|
Input: nums1 = [1,3], nums2 = [2]Output: 2.00000 Explanation: merged array = [1,2,3] and median is 2. | Input: nums1 = [1,2], nums2 = [3,4]Output: 2.50000 Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5. |
The Approach
The goal is to merge the two arrays & then pull the middle value from the array.
Since the two arrays are sorted, we apply the merge algorithm from Merge Sort to merge them into a single array.
My Solution
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int newLength = nums1.length + nums2.length;
int[] mergedSortedArray = new int[newLength];
mergedSortedArray = getMergedSortedArray(mergedSortedArray, nums1, nums2);
// Returns the middle depending whether newLength is odd or even.
if ((newLength % 2) == 0) {
int midIndex1 = (newLength - 1) / 2;
int midIndex2 = midIndex1 + 1;
return (double) (mergedSortedArray[midIndex1] + mergedSortedArray[midIndex2]) / 2;
} else {
double midIndex = Math.ceil(newLength / 2);
return (double) mergedSortedArray[(int) midIndex];
}
}
// Merges the two arrays, same principle as the merging from Merge Sort.
private int[] getMergedSortedArray(int[] mergedSortedArray, int[] nums1, int[] nums2) {
int msaIndex = 0;
int nums1Index = 0;
int nums2Index = 0;
// Copies over the smaller value between the two arrays.
while ((nums1Index < nums1.length) && (nums2Index < nums2.length)) {
int nums1Value = nums1[nums1Index];
int nums2Value = nums2[nums2Index];
if (nums1Value == nums2Value) {
mergedSortedArray[msaIndex] = nums1Value;
nums1Index++;
msaIndex++;
mergedSortedArray[msaIndex] = nums2Value;
nums2Index++;
msaIndex++;
} else if (nums1Value < nums2Value) {
mergedSortedArray[msaIndex] = nums1Value;
nums1Index++;
msaIndex++;
} else {
mergedSortedArray[msaIndex] = nums2Value;
nums2Index++;
msaIndex++;
}
}
// Copies over the remaining values.
while (nums1Index < nums1.length) {
mergedSortedArray[msaIndex] = nums1[nums1Index];
nums1Index++;
msaIndex++;
}
while (nums2Index < nums2.length) {
mergedSortedArray[msaIndex] = nums2[nums2Index];
nums2Index++;
msaIndex++;
}
return mergedSortedArray;
}
}
We first declare & instantiate mergedSortedArray, which will hold the merged nums1 & nums2 array.
getMergedSortedArray() runs the merge algorithm from Merge Sort & returns the merged array.
We then check if the length of mergedSortedArray is odd or even, then pull the middle value respectively.
Alternative solution using Binary Search.
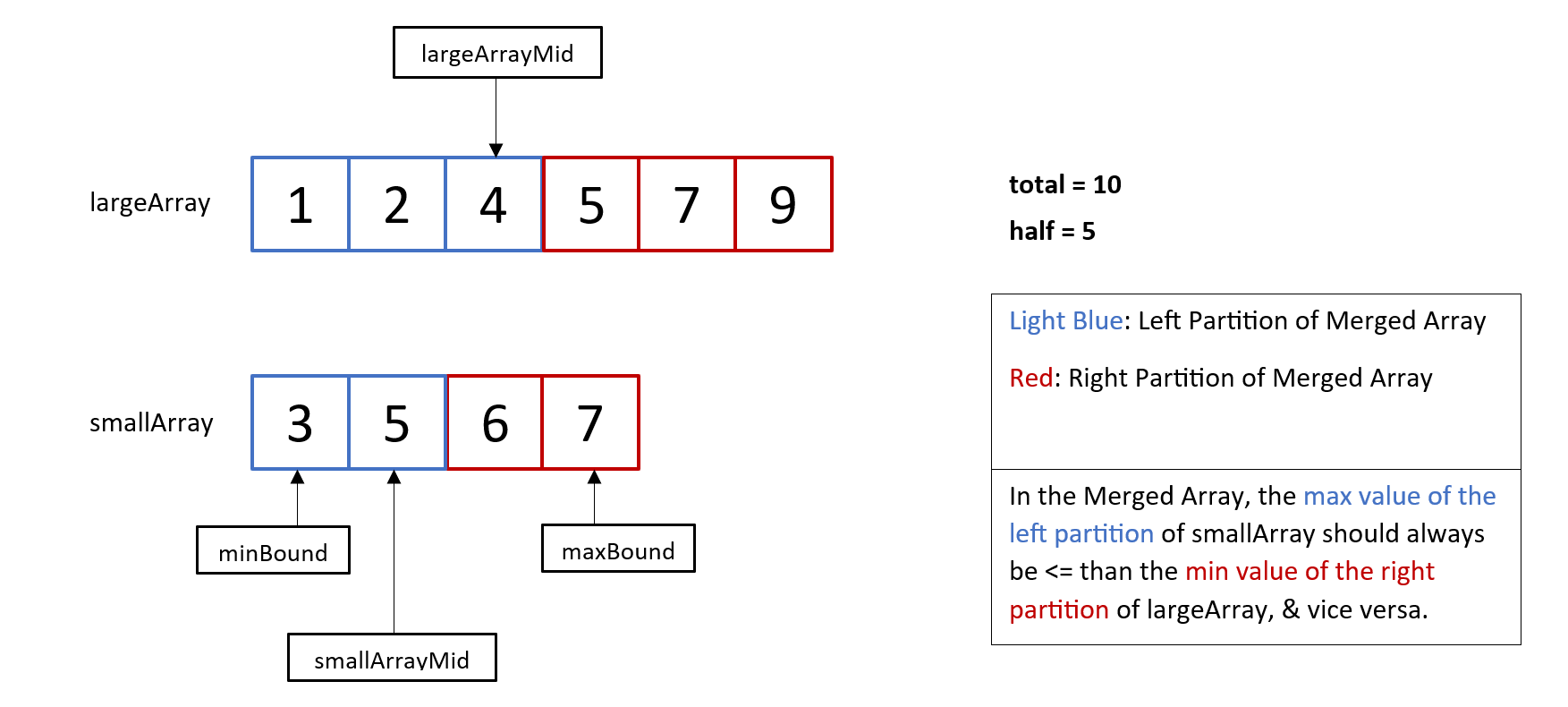
Illustration created by me.
My Solution
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
// Ensures that smallArray contains the smaller array.
int[] smallArray = nums1;
int[] largeArray = nums2;
if (nums2.length < nums1.length) {
smallArray = nums2;
largeArray = nums1;
}
int total = nums1.length + nums2.length;
int half = (total + 1) / 2; // +1 to round up the values.
// Binary Search on the smaller array.
int maxBound = smallArray.length - 1;
int minBound = 0;
// Guranteed to find a solution, thus a while true loop.
while (true) {
int smallArrayMid = (int) Math.floor((maxBound + minBound) / 2.0);
// -2 for OBOE error from calculating half.
int largeArrayMid = half - smallArrayMid - 2;
int smallLeftMax;
if (smallArrayMid >= 0) {
smallLeftMax = smallArray[smallArrayMid];
} else {
smallLeftMax = Integer.MIN_VALUE;
}
int smallRightMin;
if ((smallArrayMid + 1) < smallArray.length) {
smallRightMin = smallArray[smallArrayMid + 1];
} else {
smallRightMin = Integer.MAX_VALUE;
}
int largeLeftMax;
if (largeArrayMid >= 0) {
largeLeftMax = largeArray[largeArrayMid];
} else {
largeLeftMax = Integer.MIN_VALUE;
}
int largeRightMin;
if ((largeArrayMid + 1) < largeArray.length) {
largeRightMin = largeArray[largeArrayMid + 1];
} else {
largeRightMin = Integer.MAX_VALUE;
}
// Solution is where the max value of the left partition of smallArray is
// greater than the min value of the right partition of the larger array.
boolean outcome =
(smallLeftMax <= largeRightMin) && (largeLeftMax <= smallRightMin);
if (outcome) {
return checkIfOddorEvenThenGetMedian(
total, smallRightMin, smallLeftMax, largeRightMin, largeLeftMax
);
} else if (smallLeftMax > largeRightMin) {
maxBound = smallArrayMid - 1;
} else {
minBound = smallArrayMid + 1;
}
}
}
// Returns the median, checking if total is odd or even.
private double checkIfOddorEvenThenGetMedian(
int total, int smallRightMin, int smallLeftMax, int largeRightMin, int largeLeftMax
) {
if ((total % 2) == 0) {
double median = (Math.max(smallLeftMax, largeLeftMax) +
Math.min(smallRightMin, largeRightMin)) / 2.0;
return median;
} else {
return (double) Math.max(smallLeftMax, largeLeftMax);
}
}
}
Here is a great video that explains this approach in-depth.