NeetCode 150: Trapping Rain Water

Published: at 07:11 PM

Table of contents

Open Table of contents

The Problem

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

A Visual Example

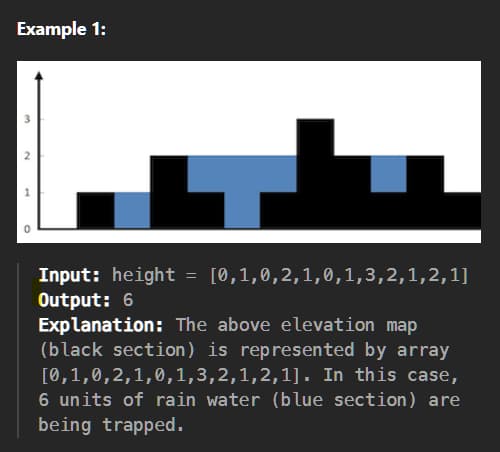
image

Image taken from LeetCode.

The Approach

The goal is to find a difference in elevation, then checking if the left or right boundaries support this containment of this difference. As such, we employ the Two Pointer method to traverse height, keeping a log of the tallest left & right boundaries seen.

If the height of the left pointer is smaller than the height at the right pointer, we compare the height at the right pointer with the max left height seen so far, taking the smaller value. We then calculate the differnce between this value and the height of the left pointer to determine the delta (i.e how many units of water can be stored). Vice versa for when l > r.

If there is no difference between height of the left pointer & the height at the right pointer, there is no delta (i.e flat surface), so only move the left pointer foward (to reduce the occurence of this case).

My Solution

class Solution {
    public int trap(int[] height) {
        if (height.length == 0) {
            return 0;
        }
        
        // Initialize the left & right pointers.
        int l = 0;
        int r = height.length - 1;

        // Variables that keep track of the maxLeft, maxRight & total.
        int maxLeftSeenSoFar = height[l];
        int maxRightSeenSoFar = height[r];
        int totalTrappedWater = 0;

        while (l < r) {
            int currentLeft = height[l];
            int currentRight = height[r];
            
            // Update the maxLeft & maxRight if required, this sets the extreme boundaries.
            maxLeftSeenSoFar = getGreaterValue(currentLeft, maxLeftSeenSoFar);
            maxRightSeenSoFar = getGreaterValue(currentRight, maxRightSeenSoFar);

            // There are 3 scenarios that can occur:
            // 1) If equal: No delta (flat surface in the POV of ONLY currentLeft & currentRight), only move l foward.
            // 2) If currentLeft < currentRight: Get the smaller of maxLeft & currentRight (enabling factor) to find the difference.
            // 3) If currentLeft > currentRight: Get the smaller of maxRight & currentLeft (enabling factor) to find the difference.
            if (currentLeft == currentRight) {
                l++;

            } else if (currentLeft < currentRight) {
                totalTrappedWater += getSmallerValue(maxLeftSeenSoFar, currentRight) - currentLeft;
                l++;

            } else {
                totalTrappedWater += getSmallerValue(maxRightSeenSoFar, currentLeft) - currentRight;
                r--;
            }
        }
        return totalTrappedWater;
    }


    // Returns the greater value.
    private int getGreaterValue(int a, int b) {
        if (a > b) {
            return a;
        } else {
            return b;
        }
    }


    // Returns the smaller value.
    private int getSmallerValue(int a, int b) {
        if (a < b) {
            return a;
        } else {
            return b;
        }
    }
}

We first initialize the left & right pointers at the opposite ends of the array, l & r respectively.

maxLeftSeenSoFar & maxRightSeenSoFar are initialized to the leftmost & rightmost heights of the array. totalTrappedWater, which keeps track of the total water units trapped so far is initialized to 0.

Until both pointers cross (checked using the while loop), get the height that each pointer is pointing to, updating maxLeftSeenSoFar & maxRightSeenSoFar if neccessary. The delta is also added to totalTrappedWater if a delta is found.

There are 3 scenarios in moving the pointers:

getGreaterValue() & getSmallerValue() are methods that return the greater or smaller value respectively.

At the end, return totalTrappedWater.