NeetCode 150: Largest Rectangle in Histogram

Table of contents

The Problem

Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

A Visual Example

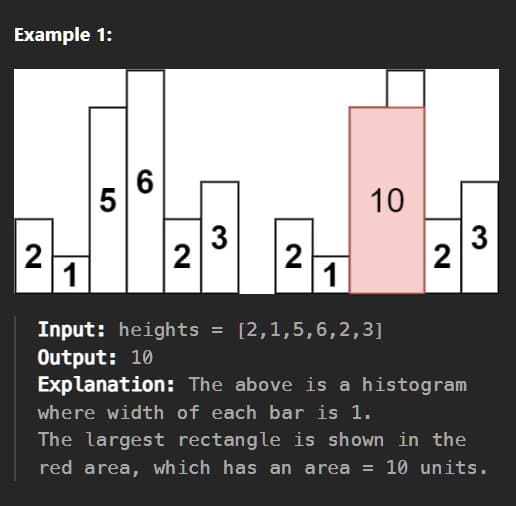
Image taken from LeetCode.

The Approach

The goal is find the largest area in the histogram by maximising one or more bars. This problem was difficult, requiring a lot of reading to figure out a valid approach.

To start, we can use a Stack to keep track of each bar. When a bar is smaller than the top of the stack is inserted into the stack, pop all preceeding elements & calculate the max area of that height to the bar currently at the top. The inserted bar then keeps the length of the last “popped” element as every element before it had a greater height.

At the end of the insertion (i.e. the loop), pop all current bars, where the length is the difference between its “stored” length & the length of heights[i]. This is because of the monotonic increasing stack created above, so every remaining bar can be extended to the “end”.

I highly recommend this video explanation as a supplement.

My Solution

class Solution {
    // Class that keeps a key value pair of a certain length & height.
    class LengthHeightPairs {
        public int length;
        public int height;

        public LengthHeightPairs(int l, int h) {
            length = l;
            height = h;
        }
    }


    public int largestRectangleArea(int[] heights) {
        Stack<LengthHeightPairs> barTracker = new Stack<LengthHeightPairs>();
        int largestRectangleSeenSoFar = 0;

        // Keep adding to the stack if the currentHeight > height of the top of the stack.
        for (int i = 0; i < heights.length; i++) {
            int currentHeight = heights[i];
            int startIndex = i;
            
            // If the currentHeight < height of the top of the stack, pop these pairs from the stack,
            // calculating the area (where the length is the difference b/w the indexes). Store the 
            // earliest index in startIndex (of the popped pairs), this is where the current bar can
            // be extended towards.
            while ((!(barTracker.isEmpty())) && (currentHeight < barTracker.peek().height)) {
                startIndex = barTracker.peek().length;

                int length = i - barTracker.peek().length;
                int height = barTracker.pop().height;
                largestRectangleSeenSoFar = getLargerValue(length * height, largestRectangleSeenSoFar);
            }
            barTracker.push(new LengthHeightPairs(startIndex, currentHeight));
        }

        // This pops all the "un-popped" elements. The length is the difference between its startIndex 
        // (or index) to the end of heights as a monotonic increasing stack is created from the above
        //  loop.
        while (barTracker.size() != 0) {
            int length = heights.length - barTracker.peek().length;
            int height = barTracker.pop().height;
            largestRectangleSeenSoFar = getLargerValue(length * height, largestRectangleSeenSoFar);
        }
        return largestRectangleSeenSoFar;
    }


    private int getLargerValue(int a, int b) {
        if (a > b) {
            return a;
        } else {
            return b;
        }
    }
}

Firstly, we create a class, LengthHeightPairs which acts as a holder of key-value pairs for each bar in heights.

We then loop over all the elements in heights, attempting to insert it in barTracker, which is a Stack.

For each attempted insertion, there are 2 outcomes:

• currentHeight > height of at the top of barTracker: Pop all the preceeding elements whose height is greater, calculating the max area (the length is difference b/w the indexes). Then insert the current pair where the length is the index of the last popped element.
• currentHeight < height of at the top of barTracker: Insert the bar, with its height & length (its index).

At the end of the loop, pop all the remaing bars, where the length is difference between its “stored” index & the length of the heights array, calculating the max area in the process.